The Luminal Phase-Lock | Why Rω = c Could Be the Missing Constraint

For a century, physics has chased a single story that unites quantum mechanics with gravity—and keeps missing the last chapter. Canonical and covariant quantization ran into non-renormalizability and the “problem of time”; semiclassical gravity and quantum field theory in curved spacetime explained Hawking radiation yet stopped short of full unification. String theory promised a UV-finite framework with extra dimensions; loop quantum gravity aimed for background independence via spin networks; asymptotic safety sought a nontrivial UV fixed point; causal dynamical triangulations, noncommutative geometry, and twistor theory offered fresh mathematical routes; holography (AdS/CFT) reframed gravity as an emergent boundary theory; and “induced/emergent gravity” à la Sakharov or Verlinde recast curvature as collective behavior. Despite these advances, a clean, testable bridge from quantum phase to gravitational inertia remains elusive—this is where a luminal phase-lock Rω=c offers a different starting constraint rather than another elaborate mechanism.

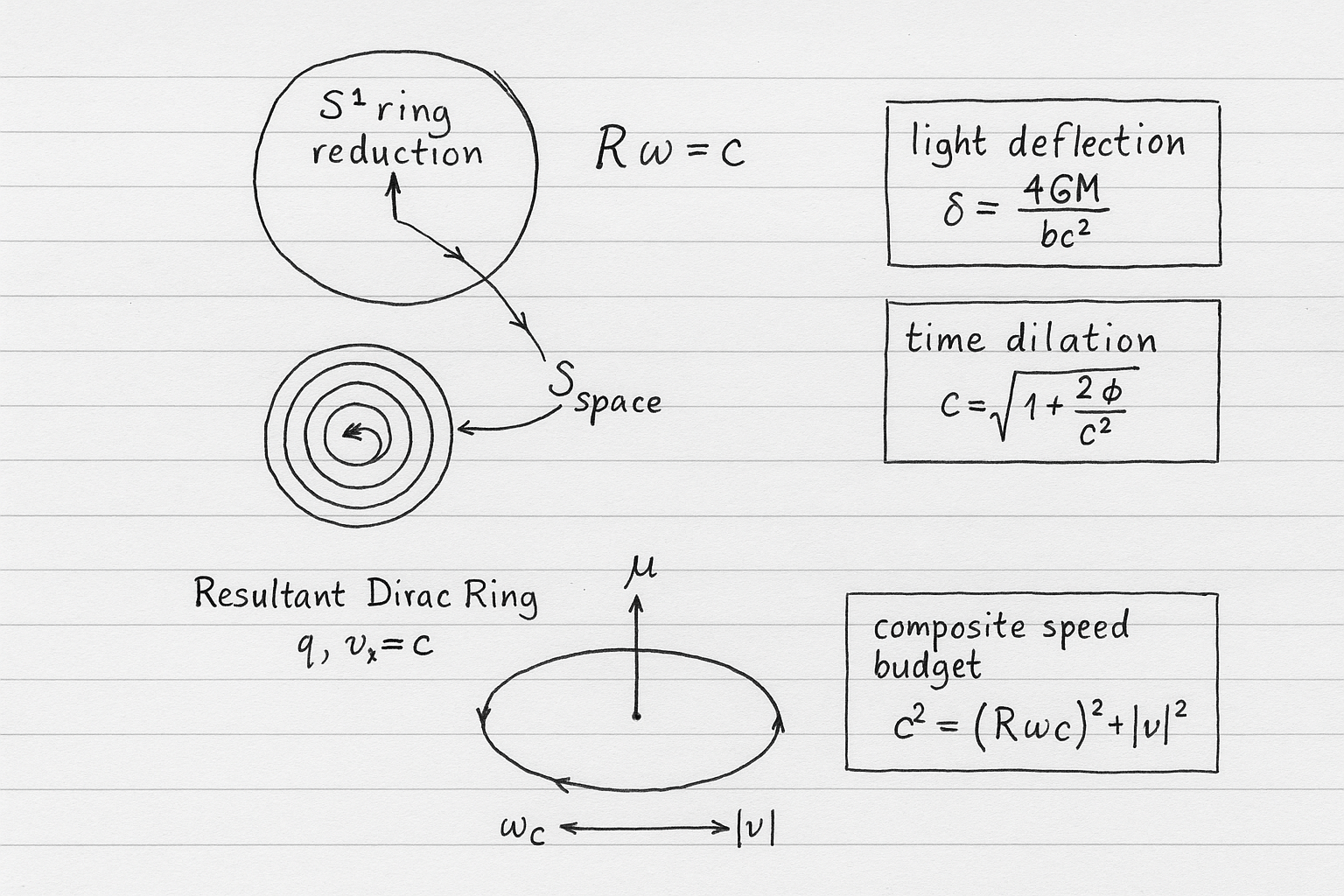
Most physics stories begin with a principle so simple you can write it in the margin of a notebook. Here, that line is “Rw= c.” Read it as a ; the internal phase of a quantum object advances as if it lives on a circular “generator” space while the particle itself propagates in ordinary three-dimensional space, and the two stay locked at light speed. In plain terms, you impose a single, global kinematic constraint at the boundary between inner phase and outer motion—and watch structure fall out. The paper lays out the postulate, the geometry, and the rules of the game with enough clarity that a motivated reader can trace every assumption back to first principles. (Core paper — DOI · ResearchGate )

What makes this worth your attention is not a new field stuffed with adjustable knobs, but the opposite; parsimony. With the luminal lock enforced across the two spaces—phase on a complex ring, motion in physical space—you recover familiar kinematics and see how inertial behavior can emerge without importing the full machinery of four-dimensional spacetime or postulating extra forces. The manuscript walks through the construction carefully; define the coupled spaces, state the invariances, set the boundary condition, and derive testable consequences. Along the way it sketches how special- and general-relativistic effects can be reinterpreted through this lock rather than assumed, and it frames the approach to constants as outcomes of geometry and balance rather than inputs.

If you are new to the framework, start with the short narrative in the DOI version above; it is the canonical reference and citable. Use the ResearchGate page to follow updates and community questions as the program expands to concrete closures—fine-structure behavior, inertial mass relations, and ultimately gravity links built from the same lock. The promise here is a reproducible route; one postulate, two coupled spaces, and no arbitrary tunings. If that sounds audacious, it is; but the paper earns the right to make the claim by laying out the path step by step.